Polynomial Division Over Field

Now your mental gymnastics must include both additive inverses and multiplicative inverses. As usual we shall omit the in multiplication when convenient The set Fx equipped with the operations and is the polynomial ring in polynomial ring xover the eld F.

Dividing Polynomials College Algebra

Dividing polynomials defined over a finite field is a little bit more frustrating than performing other arithmetic operations on such polynomials.

Polynomial division over field. Except at the end you put square brackets around the coefficients. Because the polynomial x23 that we are dividing by is monic lead coefficient 1 the division goes exactly like ordinary polynomial division. Consider again the polynomials defined over GF7.

In this video we discuss some important results concerning factorization of polynomials in a ring of polynomials over a Field. The polynomials having degree two or three are reducible if they have any root in the corresponding field. For polynomials a x b x and g x which are over the same field we say a x is congruent to b x modulo g x written a x b x mod g x if m x divides a x - b x.

Let F cdot be a field and let f g in Fx with gx neq 0. Algebraically dividing polynomials over a Galois field is equivalent to deconvolving vectors containing the coefficients of the polynomials. Is there a package like polynom for typesetting polynomial long division but over a finite field such as GF2.

Group Theory 71 Polynomial Rings Division Algorithm. A_nxn where the coefficients a_0 a_1 a_n in F. Extended polynomial GCD in finite field The calculator computes extended greatest common divisor for two polynomials in finite field person_outline Anton schedule 2019-08-19 111244.

Then there exists unique q r in Fx such that fx gxqx rx with the property that either rx 0 or degr degg. Fis the eld of coe cients of Fx. If we attempt to perform polynomial division over a coefficient set that is not a field we find that division is not always defined.

However the vertical spacing between each line and exponents of the equation below it is quite small how to increase it. Theorem 1 The Division Algorithm for Polynomials over a Field. I attempted the following solution.

And you may for example wish to replace 47 say by 5 or -2. The remainder R of N with respect to P is a polynomial of degree r such that r is less than the minimum power of N and 0r. In these polynomial rings.

A Polynomial over F is an equation of the form fx a_0 a_1x. 2x2 2 mod x2 -1. For example all polynomials are over GF 3.

To divide elements of a Galois field you can also use gfdiv instead of gfdeconv. Especially over a finite field where you dont have to worry about fractional coefficients working over for instance the rational numbers these can get extremely unwieldy surprisingly soon. Click the blue arrow to submit and see the result.

In these polynomial rings. Let F cdot be a field. Coe cients Polynomial rings over elds have many of the properties enjoyed by elds.

Polynomial long division is the way to go. It divides polynomials over a Galois field. If not how to manually typeset long division in general.

We have the division algorithm greatest common divisors least common multiples etc. Lets say we want to divide 5x2 4x 6 by 2x 1. The polynomial division calculator allows you to take a simple or complex expression and find the quotient and remainder instantly.

Enter the expression you want to divide into the editor. Since for each m 1 of Z the ring Zm Z hmi is least common multiples etc. POLYNOMIAL ALGEBRA OVER FIELDS A-139 that axi ibxj abxj always.

For details see Multiplication and Division of Polynomials. To work in GF2 m use the deconv function of the gf object with Galois arrays. The set of all polynomials over a field F is denoted Fx.

For Polynomial Division Let N and P be two polynomials over F with degrees respectively of n and p where p. The polynomial r x is called the remainder of f x modulo g x.

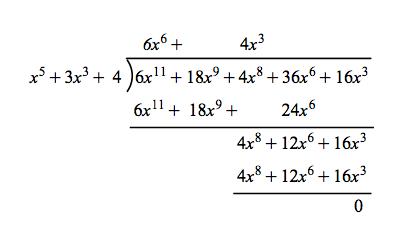
Galois Theorem And Polynomial Arithmetic

Factoring Polynomials Refers To Factoring A Polynomial Into Irreducible Polynomials Over A Given Field I Factoring Polynomials Polynomials Common Core Algebra

Factoring Polynomials Refers To Factoring A Polynomial Into Irreducible Polynomials Over A Given Field Factoring Polynomials Polynomials Numerical Expression

Pin On Awesome Uk Resources On Tpt

Dividing Polynomials College Algebra

Why Does Polynomial Long Division Work Quora

Pin By Christy Massman On Algebra 2 High School Math Secondary Math Middle School Math

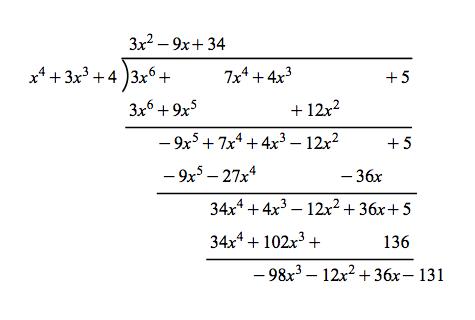
Galois Theorem And Polynomial Arithmetic

Scavenger Hunt Dividing Polynomials Long And Or Synthetic Division Polynomials Rational Function Scavenger Hunt

Factoring Using Polynomial Division Video Khan Academy

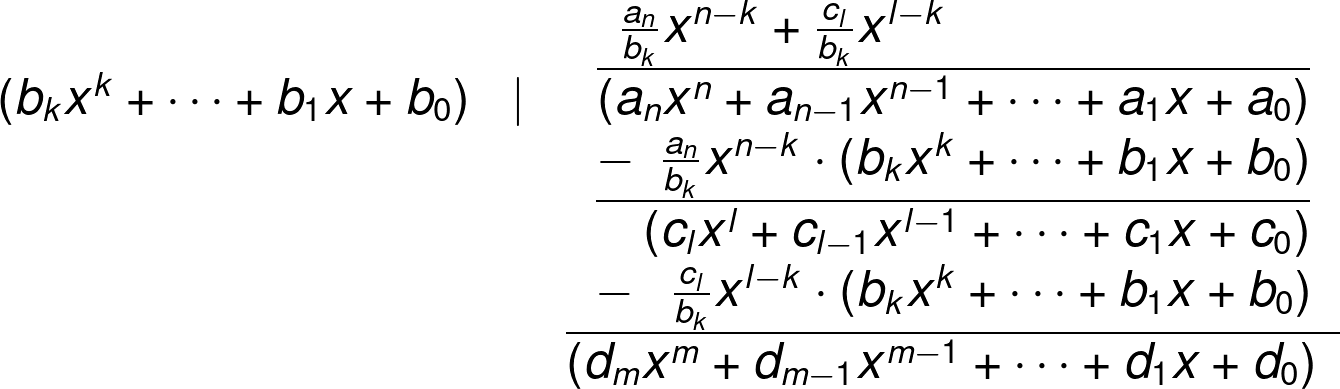
Polynomial Division Calculator

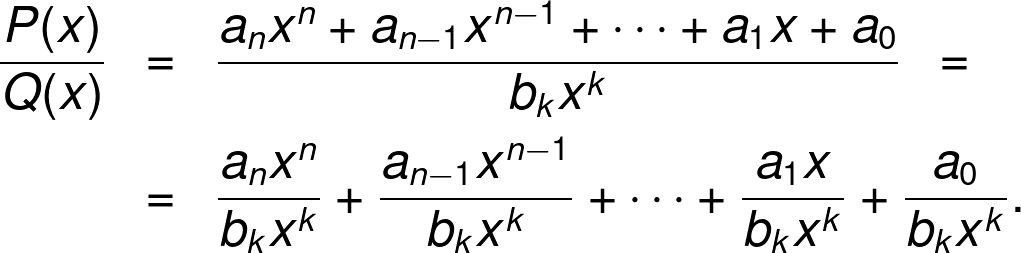
Polynomial Division Calculator

Dividing Polynomials College Algebra

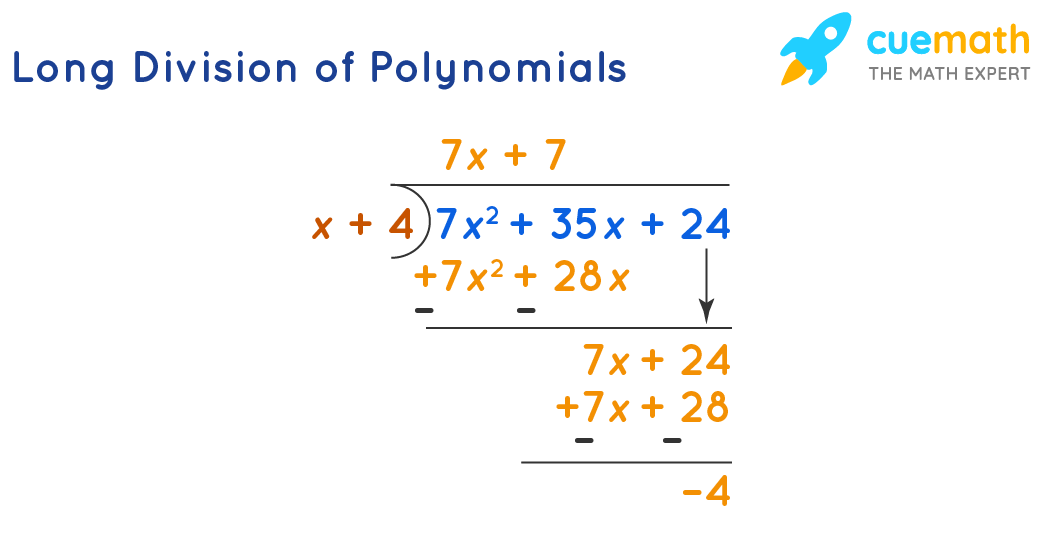
Dividing Polynomials Definition Examples Solutions Cuemath

Dividing Polynomials College Algebra

American High School Online School License Oninehighschoolforsale Onlineschoolforsale Virtualscho Online High School Online School Programs Online Education

Euclidean Division Of Polynomials Theorem And Proof Youtube

Algebra 1 Worksheets Quadratic Functions Worksheets Completing The Square Algebra Quadratics

Polynomial Long Division Over Gf P Tex Latex Stack Exchange